In the second phase (agglomeration), we have to decide how to group all the elementary computations that make up the complete job into separate tasks that we can assign to the processors. The first decision is pretty obvious: Since the Mandelbrot iteration formula feeds the result of the previous step back into the next, all the computations for one point should be performed on the same processor to avoid the need for communication among processors.

Next, we have to decide how to agglomerate the points. Since no information from other points of the image goes into the iteration formula, there is no need for communication among the points. This gives us a lot of freedom when assigning points to processors since we don't have to find an agglomeration that minimizes communication. However, in order to accommodate very large output sizes, no processor should ever have to store the whole image.

The most simple method that comes to mind would be to assign each processor a continuous block of the image. For example, with four processors, the first processor would compute the first quarter of the image, the second would compute the second quarter, and so on. This concept of blockwise agglomeration is visualized in Figure 5, where the colors and the numbers in front of each line denote the processor working on that line.

As a side note, Figure 5 also shows the solution of a minor implementation problem: Since graphical output is not available on the nodes of a parallel processing cluster, the nodes return an ASCII string for each line, where a " " character denotes a point outside the fractal set, and a "#" character denotes a point inside the set.

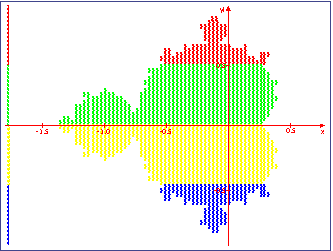
Figure 5: Blockwise agglomeration of points

Blockwise agglomeration is easy to implement, however, Figure 5 hints at a potential problem: As we can see, the largest part of the Mandelbrot set's inside is computed by processors 2 and 3, while most of the points assigned to processors 1 and 4 lie outside of the set. Since points inside the set always reach the maximum iteration count, processors 2 and 3 have a much greater workload than 1 and 4. This means that processors 1 and 4 will likely finish their computations and sit idle long before 2 and 3 are done, which is a waste of processing power if 1 and 4 can not be used for other jobs until the whole image is generated.

Consequently, we have to find a way to balance the load more evenly. A simple method to achieve this is assigning each processor not whole blocks, but alternating lines of the image, i.e. the first processor computes the first, fifth, ninth line etc, the second processor computes the second, sixth, tenth line etc., and so on (Figure 6):

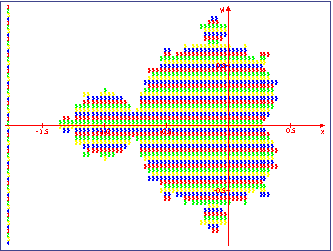
Figure 6: Linewise agglomeration of points

While this linewise agglomeration method does not balance the load precisely equally, it is a good approximation for most fractal images (unless somebody comes up with a formula that generates an image where only every fourth row is inside the set).

< Partitioning | Output Synchronization >