To demonstrate these characteristics, we zoom into the section marked by the small rectangle in Figure 2, i.e., we apply the iteration formula to every point in the area delimited by the corner coordinates

We end up with the image in Figure 3:

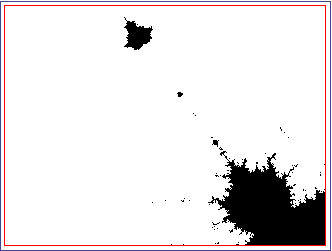
Figure 3: Mandelbrot set detail with an iteration maximum of 150

As predicted, the result is not only a magnification of the pixels from the previous image, but actually contains new, intricate detail that was not visible before. We also recognize familiar shapes, like the bulges and tendrils on the edge of the set, and even a smaller, rotated image of the Mandelbrot set at the top of this section.

The image looks a bit "dirty" like a bad photocopy, though – the edges are not clearly defined, and there are black points scattered outside the solid interior. The reason is that this image was computed with an iteration maximum of 150 – i.e., if Z did not escape to infinity after 150 iterations, the point is considered be part of the Mandelbrot set. However, we can imagine that there are points which take a many more iterations, like 1,000 or even more, to escape to infinity. These points would have been mistakenly colored black in the above image.

So, we recalculate the image, and this time iterate up to 1,500,000 times over each point before we decide that Z indeed does not escape to infinity. The result is shown in Figure 4:

Figure 4: Mandelbrot set detail with an iteration maximum of 1,500,000

The image is much clearer now; the bulges and the small replica of the Mandelbrot set are clearly discernible. We note that the higher the iteration count, the higher the accuracy of the fractal image.

< The Mandelbrot Set | Parallel Algorithm Design >